8. Applications of Differential Equations

Exercises

a. Exponential Growth and Decay

A population $P$ of deer on a small island is growing at a rate given by $P'(t)=.05P(t)$, where $t$ is time in years. If there are $680$ deer on the island now, solve the differential equation to find the population size as a function of $t$. When will the deer population reach $1000$?

$P(t)=680e^{.05t}$
$P=1000$ when $t\approx 7.7$ years

We start with the given equation: \[ \dfrac{dP}{dt}=.05P \] We separate variables and integrate: \[\begin{aligned} \int\dfrac{dP}{P}&=\int .05\,dt \\ \ln|P| &=.05t+C \end{aligned}\] To solve for $P$, we exponentiate and remove the absolute value: \[ P=\pm e^{.05t+C}=\pm e^Ce^{.05t}=Ae^{.05t} \] where $A=\pm e^C$. To solve for $A$, we plug the initial value, $P(0)=680$, into the equation: \[ 680=Ae^{.05(0)}=A \] We plug in $A=680$ to get the equation for the population size as a function of $t$: \[ P=680e^{.05t} \] To find the time when the deer population reaches $1000$, we set $P=1000$ and solve for $t$: \[\begin{aligned} 1000&=680e^{.05t} \\ 1.47&\approx e^{.05t} \\ \ln(1.47)&\approx.05t \\ t&\approx\dfrac{\ln(1.47)}{.05}\approx 7.7 \ \text{years} \end{aligned}\]

sy,jb
In living organisms, the proportion of Carbon-14 to Carbon-12 is constant. When the organism dies, the radioactive Carbon-14 begins to decay while the Carbon-12 remains the same. Thus scientists can date a fossil by comparing the proportion of these two carbons with that in living organisms.
Assuming that Carbon-14 decays at a rate proportional to the amount present, and knowing that the half-life of Carbon-14 is $5730$ years, how old is a bone fossil that contains $30\%$ of the Carbon-14 it contained at the time of death?

$t\approx 9952.8$ years

We start with the equation for exponential decay: \[ \dfrac{dQ}{dt}=-kQ \] We separate variables and integrate: \[\begin{aligned} \int\dfrac{dQ}{Q}&=\int -k\, dt \\ \ln |Q|&=-kt+C \\ \end{aligned}\] To solve for $Q$, we exponentiate and remove the absolute value: \[ Q=\pm e^{-kt+C}=\pm e^Ce^{-kt}=Ae^{-kt} \] where $A=\pm e^C$. At the time the organism died, $t=0$, the amount of Carbon-14 is \[ Q(0)=Ae^0=A \] After $5730$ years, there will be half as much left. So \[ Q(5730)=\dfrac{A}{2}=Ae^{-k5730} \] We solve for $k$: \[\begin{aligned} e^{-5730k}&=\dfrac{1}{2} \\ 5730k&=-\ln\left(\dfrac{1}{2}\right)=\ln(2) \\ k&=\dfrac{\ln(2)}{5730} \end{aligned}\] We plug this into the equation for quantity of Carbon-14 as a function of time $t$: \[ Q=Ae^{-(\ln(2)/5730)t} \] At the present time, $t=t_o$, The amount of Carbon-14 is reduced to $30\%$. We set $Q(t_o)=.3A$ and solve for $t_o$: \[\begin{aligned} Ae^{-(\ln(2)/5730)t_o}&=.3A \\ -\dfrac{\ln(2)}{5730}t_o&=\ln(.3) \\ t_o=-\dfrac{5730\ln(.3)}{\ln(2)}&\approx 9952.8 \ \text{years} \end{aligned}\]

sy,jb

Since the half-life is $7530$, we immediately know the amount after $t$ years will be \[ Q=A\left(\dfrac{1}{2}\right)^{t/5730} \] So after $t_o$, the amount will be $30\%$, or: \[ A\left(\dfrac{1}{2}\right)^{t_o/5730}=.3A \] which leads to the same solution.
The world population recently passed $6$ billion. If it took $10$ years for the world population to increase from $5$ to $6$ billion, how long will it take to increase another billion?

Assuming exponential growth, the population will grow another billion in about $8.45$ years.

We start with the equation for exponential growth: \[ P(t)=Ae^{kt} \] To solve for $A$, we plug in the initial value, $P(0)=5 \times 10^9$: \[\begin{aligned} 5\times 10^9&=Ae^{k(0)}=A\\ \end{aligned}\] So the population is: \[ P=(5\times 10^9)e^{kt} \] To solve for $k$, we plug in $P(10)=6\times 10^9$: \[\begin{aligned} 6\times 10^9 &=(5\times 10^9)e^{10k} \\ 1.2&=e^{10k} \\ k&=\dfrac{\ln(1.2)}{10} \end{aligned}\] So the population formula becomes: \[ P=(5\times 10^9)e^{(\ln(1.2)/10)t} \] To find the time when the population reaches $7$ billion, we plug in $P(t)=7\times 10^9$ and solve for $t$: \[\begin{aligned} 7\times 10^9 &=(5\times 10^9)e^{(\ln(1.2)/10)t} \\ 1.4&=e^{(\ln(1.2)/10)t} \\ \ln(1.4)&=\dfrac{\ln(1.2)}{10}t \\ t&=\dfrac{10\ln(1.4)}{\ln(1.2)}\approx 18.45 \end{aligned}\] This is the time between $5$ billion and $7$ billion, but the question is asking for the time between $6$ billion and $7$ billion. So we subtract $10$ to get $8.45$ years.

sy,jb
Suppose $P_o=$ $$5000$ is deposited in a money market account at $5\%$ annual interest, compounded continuously. If $P(t)$ is the compounded amount after $t$ years, compute and interpret $P'(4).$

$P'(4)=250e^{.2}\approx 305.35$
After $t=4$ years, this investment is increasing at the rate of $$305.35$ per year.

The formula for a principal compounded continuously is \[ P(t)=P_oe^{rt} \] where $P_o$ is the initial principal, $r$ is the rate of interest written as a decimal rather than a percent, $t$ is the time it is compounding, and $P(t)$ is the principal after time $t$. We plug in the initial value, $P_o=5000$, and the interest rate, $k=.05$, to get: \[ P(t)=5000e^{.05t} \] We then take the derivative and plug in $t=4$: \[\begin{aligned} P'(t)&=250e^{.05t} \\ P'(4)&=250e^{.2}\approx 305.35 \end{aligned}\] This means that at time $t=4$ years, this investment is increasing at the rate of $$305.35$ per year.

sy,jb

b. Newtonian Heating and Cooling

A cup of coffee is poured from a pot at the temperature of $200^{\circ}F$, and placed in a room at $70^{\circ}F$. If $2$ minutes later the temperature of the coffee is $180^{\circ}F$, when will the temperature reach $100^{\circ}F$?

$t\approx 18.09$ minutes

By Newton's law, the temperature satisfies the differential equation: \[ \dfrac{dT}{dt}=-k(T-70) \] We separate variables and integrate: \[\begin{aligned} \int\dfrac{dT}{T-70}&=\int -k\,dt \\ \ln|T-70|&=-kt+C \end{aligned}\] To solve for $T$, we exponentiate and remove the absolute value: \[\begin{aligned} |T-70|&=e^{-kt}e^C \\ T-70&=\pm e^{-kt}e^C \\ T&=Ae^{-kt}+70 \end{aligned}\] where $A=\pm e^C$. To solve for $A$, we plug in the initial value, $T(0)=200$: \[\begin{aligned} 200&=Ae^{-k(0)}+70=A+70 \\ A&=130 \\ \end{aligned}\] Substituting back, we get: \[ T=130e^{-kt}+70 \] To find $k$, we plug in $T(2)=180$: \[\begin{aligned} 180&=130e^{-2k}+70 \\ e^{-2k}&=\dfrac{110}{130}\approx.85 \\ k&=-\,\dfrac{\ln(.85)}{2}\approx.0813 \end{aligned}\] So the temperatute at time $t$ is: \[ T(t)=130e^{-.0813t}+70 \] To find the time when the temperature reaches $100$, we set $T(t)=100$ and solve for $t$: \[\begin{aligned} 100&=130e^{-.0813t}+70 \\ e^{-.0813t}&=\dfrac{30}{130}=.23 \\ -.0813t&=\ln{.23} \\ t&=-\,\dfrac{\ln(.23)}{.0813}\approx 18.09 \ \text{minutes} \end{aligned}\]

sy,jb
A rib-eye roast at room temperature, $72^{\circ}F$, is placed in a $350^{\circ}F$ oven at time $t=0.$ In $30$ minutes, the temperature of the roast has risen to $90^{\circ}F$.
1. Find the temperature $T(t)$ of the roast after $t$ hours.
  
  $T(t)=350-278e^{-.134t}$
  
  Newton's law of heating says $\dfrac{dT}{dt}=-k(T-350)$ or equivalently, $\dfrac{d}{dt}(T-350)=-k(T-350)$. So the solution is: \[ T-350=Ae^{-kt} \] To solve for $A$, we plug in the inital value, $T(0)=72$: \[\begin{aligned} 72-350&=Ae^{-k(0)}\\ A&=-278 \end{aligned}\] Plugging this in, we get: \[ T=350-278e^{-kt} \] To find $k$, we evaluate $T(.5)=90$: \[\begin{aligned} 90&=350-278e^{-.5k} \\ e^{-.5k}&=\dfrac{-260}{-278}=.935 \\ k&=-2\ln(.935)=.134 \end{aligned}\] So the temperature of the roast after $t$ hours is: \[ T(t)=350-278e^{-.134t} \]
  
  sy,jb
2. What is the temperature of the roast after one hour?
  
  $T(1)\approx 106.9^{\circ}$
  
  We plug $t=1$ into the temperature from the previous part: \[ T(1)=350-278e^{-.134}\approx 106.9^{\circ} \]
  
  sy,jb
3. How long will it take to cook the roast to medium - with a temperature of $145^{\circ}F$?
  
  $t\approx 2.27$ hours
  
  We plug in $T(t)=145$ and solve for $t$: \[\begin{aligned} 145&=350-278e^{-.134t} \\ e^{-.134t}&=\dfrac{-205}{-278}=.737 \\ t&=\dfrac{\ln(.737)}{-.134}\approx 2.27 \ \text{hours} \end{aligned}\]
  
  sy,jb
A hunter shoots a deer. At $1.5$ hours after the deer is shot, its body temperature is $85^{\circ}F$. At $3$ hours after the deer is shot, its body temperature is $77^{\circ}F$. The ambient tempertature is $69^{\circ}F$. Find the natural body temperature of the deer.

$T\approx 101^{\circ}F$

Newton's law of cooling says $\dfrac{dT}{dt}=-k(T-69)$. Equivalently, $\dfrac{d}{dt}(T-69)=-k(t-69)$. So the solution is: \[ T-69=Ae^{-kt} \] To find $A$ and $k$, we plug in $T(1.5)=85$ and $T(3)=77$ to get two equations: \[ 85-69=16=Ae^{-1.5k}\quad\text{and }\quad 85-77=8=Ae^{-3k} \] To solve the system of equations, we divide the first equation by the second one: \[ 2=\dfrac{e^{-1.5k}}{e^{-3k}}=e^{1.5k} \] So \[ k=\dfrac{\ln2}{1.5}\approx.462 \] Substituting $e^{1.5k}=2$ back into the equation $16=Ae^{-1.5k}$ we find: \[ A=32 \] Therefore, \[ T=69+32e^{-.462t} \] At $t=0$, we find the initial body temperature of the deer is: \[ T(0)=69+32=101^{\circ}F \]

jb

c. Mixing Problems

A $5$ pound box of soap has been dumped into the campus fountain that contains $500$ gal of water. To clean up the mess, maintenance personnel run fresh water into the fountain at the rate of $15$ gal per minute allowing the well-mixed solution to drain off at the same rate. How long will it take to reduce the amount of soap in the fountain to $0.5$ pounds?

$t\approx 76.8\text{ min}$

Let $S(t)$ be the amount of soap in the fountain as a function of time. The differential equation says the rate of change of the amount of soap is the amount “in” minus the amount “out”. Since there is no soap in the pure water going in and there are $S\text{ lb}$ of soap in the $500\text{gal}$ of water, the equation is: \[\begin{aligned} \dfrac{dS}{dt}&=0\dfrac{\text{lb}}{\text{gal}}15 \dfrac{\text{gal}}{\text{min}}-\dfrac{S}{500}\dfrac{\text{lb}}{\text{gal}}15\dfrac{ \text{gal}}{\text{min}} \\ \dfrac{dS}{dt}&=-.03S \end{aligned}\] Since this is just exponential decay, the solution is: \[ S=Ae^{-.03t} \] To solve for $A$, we plug in the initial value, $S(0)=5$: \[ 5=Ae^{-.03(0)}=A \] So the equation is: \[ S(t)=5e^{-.03t} \] To find the time at which there are $0.5\text{ lb}$ of soap, we plug in $S(t)=0.5$ and solve for $t$: \[\begin{aligned} .5&=5e^{-.03t} \\ .1&=e^{-.03t} \\ t&=-\dfrac{\ln(.1)}{.03}\approx 76.8\text{ min} \end{aligned}\]

sy,jb
A $100$ gal tank contains $20$ lb of salt. A solution containing $.05$ lb salt / gal is added at the rate of $8$ gal/min. The solution is well mixed and withdrawn at the rate of $8$ gal/min.
1. How much salt is present in the solution after $90$ minutes?
  
  $S\approx 5.01\ \text{lb}$
  
  Let $S(t)$ be the amount of salt in the tank as a function of time. The differential equation for the rate of change of the amount of salt is: \[\begin{aligned} \dfrac{dS}{dt}&=.05\dfrac{\text{lb}}{\text{gal}}8\dfrac{\text{gal}}{\text{min}} -\dfrac{S}{100}\dfrac{\text{lb}}{\text{gal}}8\dfrac{\text{gal}}{\text{min}} \\ \dfrac{dS}{dt}&=.4-.08S \end{aligned}\] We put it into standard form: \[ \dfrac{dS}{dt}+.08S=.4 \] To solve, we find an integrating factor and multiply it on both sides: \[ I=e^{\textstyle \int.08\,dt}=e^{.08t} \] \[ e^{.08t}\dfrac{dS}{dt}+.08e^{.08t}S=.4e^{.08t} \] We recognize the left side as the derivative of a product, integrate both sides and solve for $S$: \[\begin{aligned} \dfrac{d}{dt}\left(e^{.08t}S\right)&=.4e^{.08t} \\ e^{.08t}S&=\int.4e^{.08t}\,dt=5e^{.08t}+C \\ S&=5+Ce^{-.08t} \end{aligned}\] To find $C$, we use the initial condition, $S(0)=20$: \[\begin{aligned} 20&=5+Ce^{-.08(0)}=5+C \\ C&=15 \end{aligned}\] So the solution is: \[ S=5+15e^{-.08t} \] To find the amount of salt present after $1.5$ hours, we plug in $t=90$ and solve for $S$: \[\begin{aligned} S&=5+15e^{-.08(90)}=5+15e^{-7.2} \\ S&\approx 5.01\ \text{lb} \end{aligned}\]
  
  sy,jb
2. What is the initial concentration, the concentration as a function of $t$ and the concentration at large times?
  
  $\displaystyle C(0)=.2\dfrac{\text{ lb}}{\text{ gal}}$
  $\displaystyle C(t)=\left(.05+.15e^{-.08t}\right)\dfrac{\text{ lb}}{\text{ gal}}$
  $\displaystyle \lim_{t\to\infty}C(t)=.05\dfrac{\text{ lb}}{\text{ gal}}$
  
  The initial concentration is: \[ C(0)=\dfrac{S(0)}{100\text{ gal}}=\dfrac{20\text{ lb}}{100\text{ gal}} =.2\dfrac{\text{ lb}}{\text{ gal}} \] As a function of time, the concentration is: \[\begin{aligned} C(t)&=\dfrac{S(t)}{100\text{ gal}}=\dfrac{1}{100}\left(5+15e^{-.08t}\right) \\ &=\left(.05+.15e^{-.08t}\right)\dfrac{\text{ lb}}{\text{ gal}} \end{aligned}\] At large times, we take the limit of the concentration as $t$ approaches infinity: \[ \lim_{t\to\infty}C(t) =\lim_{t\to\infty}\left(.05+.15e^{-.08t}\right)=.05\dfrac{\text{ lb}}{\text{ gal}} \] Notice that this is the same as the concentration of the salt water solution going in.
  
  sy,jb
A $100$ gal tank contains $50$ gal of distilled water. Starting at time $t=0$, a solution containing $.25$ lb of food coloring per gal is added to the tank at $3$ gal/min. The contents are kept well stirred and the mixture is withdrawn at the rate of $2$ gal/min. Note the volume is not constant in this problem.
1. Find the amount of food coloring present as a function of time, $t$ min.
  
  First find the volume as a function of time. Then the differential equation is linear but not separable.
  
  $\displaystyle S(t)=.25(50+t)-\dfrac{31250}{(50+t)^2}$
  
  In this problem, the volume is not constant, $3$ gal/min is being added while $2$ gal/min is coming out. So the volume $V$ at time $t$ is: \[ V(t)=50+3t-2t=50+t \] Let $F(t)$ be the amount of food coloring in the tank as a function of time. The differential equation for the rate of change of the amount of food coloring is: \[ \dfrac{dF}{dt}=.25\dfrac{\text{lb}}{\text{gal}}3\dfrac{\text{gal}}{\text{min}} -\dfrac{F}{V}\dfrac{\text{lb}}{\text{gal}}2\dfrac{\text{gal}}{\text{min}} \] Substituting the volume in, we get: \[ \dfrac{dF}{dt}=.75-\dfrac{2F}{50+t} \] which is linear but not separable. We put the equation in standard form: \[ \dfrac{dF}{dt}+\dfrac{2F}{50+t}=.75 \] To solve, we first find an integrating factor: \[ I=e^{\textstyle \int\frac{2}{50+t}\, dt}=e^{2\ln|50+t|}=(50+t)^2 \] We then multiply both sides by the integrating factor: \[ (50+t)^2\dfrac{dF}{dt}+2(50+t)F=.75(50+t)^2 \] We recognize the left side as the derivative of a product, integrate both sides and solve for $F$: \[\begin{aligned} \dfrac{d}{dt}\left[(50+t)^2F\right]&=.75(50+t)^2 \\ (50+t)^2F&=\int .75(50+t)^2\, dt=.25(50+t)^3+C \\ F&=.25(50+t)+\dfrac{C}{(50+t)^2} \\ \end{aligned}\] To find $C$, we plug $F(0)=0$ into the implicit form: \[\begin{aligned} 0&=.25(50)^3+C \\ C&=-31250 \\ \end{aligned}\] So the solution is: \[ F(t)=.25(50+t)-\dfrac{31250}{(50+t)^2} \]
  
  sy,jb
2. If a $30\%$ solution is desired, will this concentration be achieved before the tank is full?
  
  No. When the tank is full, it contains $21.9$ lb concentrate. Thus the solution is $21.9\%$.
  
  To find the time at which the tank in full, we plug in $V(t)=100$: \[\begin{aligned} 100&=50+t \\ t&=50 \\ \end{aligned}\] The amount of food coloring in the tank at $t=50$ is: \[ F(50)=.25(100)-\dfrac{31250}{100^2}=21.9 \] So the concentration of the solution when the tank is full is: \[ C(50)=\dfrac{F(50)}{V(50)}=\dfrac{21.9}{100}=.219=21.9\% \] Therefore, a $30\%$ solution will not yet be achieved before the tank is full.
  
  sy,jb

d. A Robot Car

The speed of a robot car satisfies $v(t)=x(t)+\dfrac{1}{x(t)}\,\dfrac{\text{m}}{\text{min}}$. If the car starts at $x(0)=\sqrt{8}$, find the time elapsed until it reaches $x=\sqrt{26}$.

$t=\dfrac{1}{2}\ln3\approx.55\ \text{min}$

The position of the car satisfies the equation: \[ v(x)=\dfrac{dx}{dt}=x+\dfrac{1}{x} \] To find the solution of this equation, we first separate variables: \[\begin{aligned} \dfrac{1}{x+\dfrac{1}{x}}dx&=dt \\ \dfrac{x}{x^2+1}dx&=dt \\ \end{aligned}\] We then integrate using the substitution $u=x^2+1$ and $du=2xdx$: \[\begin{aligned} \int\dfrac{x}{x^2+1}\,dx&=\int dt \\ \dfrac{1}{2}\int\dfrac{1}{u}\,du&=\int dt \\ \dfrac{1}{2}\ln(x^2+1)&=t+C \\ \end{aligned}\] To find $C$, we use the initial condition, $x(0)=\sqrt{8}$: \[\begin{aligned} \dfrac{1}{2}\ln(\sqrt{8}^2+1)=0+C \\ C=\dfrac{1}{2}\ln9 \\ \end{aligned}\] Substituting this in and solving for $t$, we get: \[ t=\dfrac{1}{2}\ln(x^2+1)-\dfrac{1}{2}\ln9=\dfrac{1}{2}\ln\left(\dfrac{x^2+1}{9}\right) \] To find the total elapsed time, we plug in the position of the car $x=\sqrt{26}$ m \[ t=\dfrac{1}{2}\ln\left(\dfrac{(\sqrt{26})^2+1}{9}\right) =\dfrac{1}{2}\ln3 \approx .55\ \text{min} \]

sy,jb

e. Falling near the Earth

A $5$ lb block is dropped from a height of $500$ ft. Assume the only force acting on the block is acceleration due to gravity.
1. Give its height, $y(t)$, and its velocity, $v(t)$, at time $t$ sec.
  
  $y(t)=-16t^2+500$
  $v(t)=-32t$
  
  To find $v(t)$, we start by integrating the acceleration equation, $\dfrac{dv}{dt}=-g$, where $g=32$: \[ v(t)=\int -32\, dt=-32t+C \] Since the block is dropped, $v(0)=0$. So $C=0$ and: \[ v(t)=-32t \] To find $y(t)$, we integrate $\dfrac{dy}{dt}=v(t)$: \[ y(t)=\int -32t\, dt=-16t^2+K \] The initial height is $y(0)=500$. So $K=500$ and: \[ y(t)=-16t^2+500 \]
  
  sy,jb
2. What is its velocity after $4$ sec.? What distance has it traveled in $4$ sec.?
  
  $v(4)=-128$ ft/sec
  In $4$ seconds, the block has traveled $256$ feet.
  
  To find the velocity at $4$ seconds, we plug $t=4$ into $v(t)$: \[ v(4)=-32(4)=-128 \] To find the distance traveled after $4$ seconds, we find the difference between $y(0)=500$ and $y(4)$: \[\begin{aligned} y(4)&=-16(4)^2+500=244 \\ \text{distance}\,&=y(0)-y(4)=500-244=256 \end{aligned}\]
  
  sy,jb
3. When will it hit the ground? What is its velocity when it hits the ground?
  
  $t=\sqrt{\dfrac{125}{4}}\approx 5.59$ sec
  
  To find the time at which the block will hit the ground, we set $y(t)=0$ and solve for $t$: \[\begin{aligned} 0&=-16t^2+500 \\ t^2&=\dfrac{500}{16}=\dfrac{125}{4}=31.25 \\ t&=\sqrt{\dfrac{125}{4}}\approx 5.59 \end{aligned}\]
  
  sy,jb
A $5$ lb block is dropped from a height of $500$ ft. Now assume air resistance with a drag coefficient of $.2$ lb/sec.
1. Give the position, $y(t)$, above the ground and the velocity, $v(t)$, at time $t$ sec.
  
  $y(t)=-20000e^{-.04t}-800t+20500$
  $v(t)=800e^{-.04t}-800$
  
  To find $v(t)$, we start with the velocity equation, $m\dfrac{dv}{dt}=-mg-kv$, where $m=5$, $g=32$, and $k=.2$: \[ 5\dfrac{dv}{dt}=-5(32)-.2v \] This is linear. In standard form, it is: \[ \dfrac{dv}{dt}+.04v=-32 \] To solve, we find an integrating factor and multiply it on both sides: \[ I=e^{\textstyle \int.04\,dt}=e^{.04t} \] \[ e^{.04t}\dfrac{dv}{dt}+.04e^{.04t}v=-32e^{.04t} \] We rewrite the left side as the derivative of a product, integrate both sides, and solve for $v$: \[\begin{aligned} \dfrac{d}{dt}\left(e^{.04t}v\right)&=-32e^{.04t} \\ e^{.04t}v&=-\int 32e^{.04t}\,dt=-800e^{.04t}+C \\ v(t)&=-800+Ce^{-.04t} \\ \end{aligned}\] To find $C$, we plug the initial condition $v(0)=0$ into the implicit solution: \[\begin{aligned} 0&=-800+C \\ C&=800 \\ \end{aligned}\] So the solution is: \[ v(t)=800e^{-.04t}-800 \] To find $y(t)$, we integrate $v(t)$: \[\begin{aligned} y(t)&=\int\left(800e^{-.04t}-800\right)\,dt \\ &=-20000e^{-.04t}-800t+K \end{aligned}\] To find $K$, we use the initial condition $y(0)=500$: \[\begin{aligned} 500&=-20000e^{-.04(0)}-800(0)+K \\ 500&=-20000+K \\ K&=20500 \\ \end{aligned}\] So the solution is: \[ y(t)=-20000e^{-.04t}-800t+20500 \]
  
  sy,jb
2. What is its velocity after $4$ sec.? What distance has it traveled in $4$ sec.?
  
  $v(4)\approx -118.3$ ft/sec
  After $4$ seconds, the block has traveled approximately $242.88$ feet.
  
  To find the velocity at $4$ seconds, we plug in $t=4$ to $v(t)$: \[ v(4)=800e^{-.04(4)}-800\approx -118.28 \] (The velocity is negative because it is moving downward.) To find the distance traveled after $4$ seconds, we find the difference between $y(0)=500$ and $y(4)$: \[\begin{aligned} y(4)=-20000e^{-.04(4)}-800(4)+20500\approx 257.12 \\ \text{distance}\,=y(0)-y(4)\approx 500-257.12 \approx 242.88 \end{aligned}\]
  
  sy,jb
3. When will it hit the ground? What is its velocity when it hits the ground?
  
  $y(t)=0$ when $t\approx5.8$ sec
  $v(5.8)\approx -165.6$ ft/sec
  
  To find the time it hits the ground, we solve $y(t)=0$ or \[ -20000e^{-.04t}-800t+20500=0 \] Since this is a trancendental equation, we can use a computer algebra system to approximate the solution, or approximate it graphically. See the plot at the right. The solution is approximately: \[ t\approx5.8\,\text{sec} \]
  
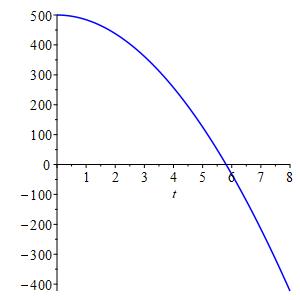
  To find the velocity when it hits the ground, we plug $t=5.8$ into the expression for $v(t)$: \[ v(5.8)=800e^{-.04(5.8)}-800\approx -165.6\ \text{ft/sec} \]
  
  sy,jb
4. What is the terminal velocity?
  
  $v_\text{terminal}=-800$ ft/sec
  
  To find the terminal velocity, we take the limit of $v(t)$ as $t$ approaches $\infty$: \[ v_\text{terminal}=\lim_{t\to\infty}\left(800e^{-.04t}-800\right)=-800 \]
  
  sy,jb

f. Logistic Growth

A lake is stocked with $500$ fish. The maximum fish population the lake can sustain is $10,000$. Assume the fish population doubles in $4$ months.
1. How many fish are in the lake at the end of $10$ months (assuming none die and none are caught)?
  
  Use the solution of the logistic growth model in the form: \[P=\dfrac{M}{1+Be^{-Mkt}}\]
  
  $P(10)\approx 2542$ fish
  
  We start with the logistic growth model and plug in $M=10000$: \[P(t)=\dfrac{M}{1+Be^{-Mkt}}=\dfrac{10000}{1+Be^{-10000kt}}\] To find $B$, we use the initial value $P(0)=500$: \[\begin{aligned} 500&=\dfrac{10000}{1+Be^{-10000k(0)}}=\dfrac{10000}{1+B} \\ 1+B&=\dfrac{10000}{500}=20 \\ B&=19 \\ \end{aligned}\] Substituting this in, we get: \[P(t)=\dfrac{10000}{1+19e^{-10000kt}}\] To find $k$, we use the given value $P(4)=1000$: \[\begin{aligned} 1000&=\dfrac{10000}{1+19e^{-40000k}} \\ 10&=1+19e^{-40000k} \\ \dfrac{9}{19}&=e^{-40000k} \\ k&=\dfrac{\ln{\left(\dfrac{9}{19}\right)}}{-40000}\approx 1.87\times 10^{-5} \\ \end{aligned}\] So the equation is: \[ P(t)=\dfrac{10000}{1+19e^{-.187t}} \] To find the population after $10$ months, we plug $t=10$ into $P(t)$: \[ P(10)=\dfrac{10000}{1+19e^{-1.87}}\approx 2542\ \text{fish} \]
  
  sy,jb
2. When is the fish population increasing most rapidly?
  
  Leaving the arbitrary constants in the model will make differentiation less odious!
  Just remember that $t$ is the only non-constant!
  
  $t\approx15.7$ months
  
  We leave the constants in the equation to make it easier to differentiate, but remember $M=10000$, $B=19$, and $k\approx 1.87\times 10^{-5}$. The population is: \[ P(t)=\dfrac{M}{1+Be^{-Mkt}}=M(1+Be^{-Mkt})^{-1} \] So the rate at which it increases is: \[\begin{aligned} P'(t)&=-M(1+Be^{-Mkt})^{-2}(-MBke^{-Mkt})\\ &=M^2Bke^{-Mkt}(1+Be^{-Mkt})^{-2} \end{aligned}\] To find the time at which the population is increasing most rapidly, we need to set the derivative of this rate equal to $0$ and solve for $t$. This means we must solve $P''(t)=0$. We use the Product Rule: \[\begin{aligned} P''(t) &=M^2Bke^{-Mkt}(-2)(1+Be^{-Mkt})^{-3}(-MBke^{-Mkt}) \\ &\quad-M^3Bk^2e^{-Mkt}(1+Be^{-Mkt})^{-2} \\ &=(1+Be^{-Mkt})^{-3}\left[2M^3B^2k^2e^{-2Mkt}-M^3Bk^2e^{-Mkt}(1+Be^{-Mkt})\right] \\ &=(1+Be^{-Mkt})^{-3}\left[2M^3B^2k^2e^{-2Mkt}-M^3Bk^2e^{-Mkt}-M^3B^2k^2e^{-2Mkt}\right] \\ &=(1+Be^{-Mkt})^{-3}\left[M^3B^2k^2e^{-2Mkt}-M^3Bk^2e^{-Mkt}\right] \\ &=\dfrac{M^3Bk^2e^{-Mkt}(Be^{-Mkt}-1)}{(1+Be^{-Mkt})^3} \\ \end{aligned}\] We set $P''(t)=0$ and solve for $t$: \[ \dfrac{M^3Bk^2e^{-Mkt}(Be^{-Mkt}-1)}{(1+Be^{-Mkt})^3}=0 \] For the fraction to equal $0$, the numerator must equal $0$, so: \[\begin{aligned} Be^{-Mkt}-1&=0 \\ e^{-Mkt}&=\dfrac{1}{B} \\ -Mkt&=-\ln B \\ t&=\dfrac{\ln B}{Mk} \\ \end{aligned}\] Plugging in $M$, $B$, and $k$, we get: \[ t=\dfrac{\ln19}{.187}\approx 15.7 \] So the fish population is increasing most rapidly at $t\approx 15.7$ months.
  
  sy,jb
Profits from a new innovation in an existing product can follow a logistic model: rapid increases at first, then tapering off over time. Let $P(t)$ be the profit per month in millions of dollars $t$ months after introduction of the innovation. If $P(0)=.5$, $P(3)=1$, and $P(6)=1.5$, what is the limiting profit per month from the sale of this product?

$M=2$, so the limiting profit is $2$ million
$P=\dfrac{2}{1+3e^{-t\ln3/3}}$

Plugging in the given values into the logistic growth model \[ P=\dfrac{M}{1+Be^{-Mkt}} \] we get $3$ equations: \[\begin{aligned} &1)\ .5=\dfrac{M}{1+B} \\ &2)\ 1=\dfrac{M}{1+Be^{-3Mk}} \\ &3)\ 1.5=\dfrac{M}{1+Be^{-6Mk}} \\ \end{aligned}\] We can use equation $1$ to solve for $B$ in terms of $M$: \[\begin{aligned} .5&=\dfrac{M}{1+B} \\ 1+B&=2M \\ B&=2M-1 \\ \end{aligned}\] We plug this into equation $2$ and solve for $k$ in terms of $M$: \[\begin{aligned} 1&=\dfrac{M}{1+(2M-1)e^{-3Mk}} \\ (2M-1)e^{-3Mk}&=M-1 \\ e^{-3Mk}&=\dfrac{M-1}{2M-1} \\ -3Mk&=\ln\left({\dfrac{M-1}{2M-1}}\right) \\ k&=-\dfrac{1}{3M}\ln\left({\dfrac{M-1}{2M-1}}\right) \\ \end{aligned}\] Finally, we plug our expressions for $B$ and $k$ into equation $3$ and solve for $M$: \[\begin{aligned} 1.5&=\dfrac{M}{1+(2M-1)e^{-6M\left(-\frac{1}{3M}\ln\left(\frac{M-1}{2M-1}\right)\right)}} \\ \dfrac{3}{2}&=\dfrac{M}{1+(2M-1)e^{2\ln\left(\frac{M-1}{2M-1}\right)}} \\ &=\dfrac{M}{1+(2M-1)\left(\frac{M-1}{2M-1}\right)^2} =\dfrac{M}{1+\frac{(M-1)^2}{2M-1}} \\ &=\dfrac{2M^2-M}{2M-1+(M-1)^2} =\dfrac{2M^2-M}{M^2} \\ 3M^2&=4M^2-2M \\ 0&=M^2-2M =M(M-2) \\ \end{aligned}\] Since we must have $M\gt0$, we conclude the limiting profit is $M=2$ million per month. So $B=3$ and $k=\dfrac{\ln3}{6}$.

Plugging in the given values into the logistic growth model \[ P=\dfrac{2}{1+3e^{-t\ln3/3}} \]

sy,jb

Review Exercises

A certain strain of bacteria grows at a rate proportional to the square of the number in the population. Set up a differential equation which describes this growth. Sketch a solution.

The differential equation which describes the growth is: $\dfrac{dP}{dt}=kP^2$
The graph of a solution is: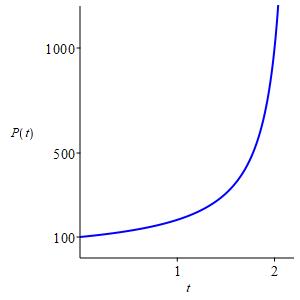

Let $P(t)$ be the number of bacteria at time $t$. The growth rate is proportional to the square of the number of bacteria, so the differential equation is: \[ \dfrac{dP}{dt}=kP^2 \] To solve, we separate variables and integrate: \[\begin{aligned} \int\dfrac{dP}{P^2}&=\int k\,dt \\ -\dfrac{1}{P}&=kt+C \\ P(t)&=\dfrac{1}{-kt+C} \\ \end{aligned}\] To find and graph a solution, we choose some plausible given conditions, say $P(0)=100$ and $P(2)=1000$. To find $C$, we plug in $P(0)=100$: \[\begin{aligned} 100&=\dfrac{1}{C} \\ C&=.01 \\ \end{aligned}\] So the equation is: \[ P(t)=\dfrac{1}{-kt+.01} \]

To find $k$, we plug in $P(2)=1000$: \[\begin{aligned} 1000&=\dfrac{1}{-2k+.01} \\ -2k+.01&=.001 \\ k&=.0045 \\ \end{aligned}\] Substituting this in, we get: \[ P(t)=\dfrac{1}{-.0045t+.01} \] The plot for this solution is:

More generally, let's keep $k=.0045$ and plot the slope field for \[ \dfrac{dP}{dt}=.0045P^2 \] and several solution curves.

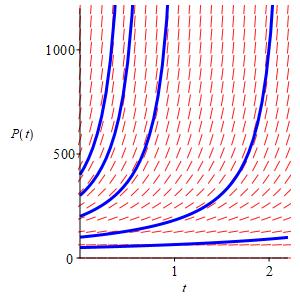
sy,jb
It has been estimated that the rate at which a person can memorize $N$ items is directly proportional to the number of items remaining to be memorized. i.e. If $y$ is the number of items memorized in time $t$, then $\dfrac{dy}{dt}=k(N-y)$ for a positive constant $k$. We'll call this a limited growth model. Assume the person can memorize the first item in $1\,\text{sec}$ and can memorize the second item in $2\,\text{sec}$ more.
1. Solve the initial value problem to express $y$ as a function of $t$. Plot the solution for $N=20$.
  
  Limited Growth: \[ y_\text{lim}=20-19\left(\dfrac{19}{18}\right)^{.5-.5t} \]
  
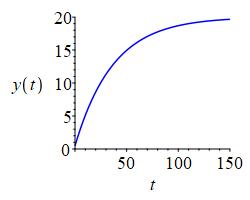
  The given equation for the rate of change of items memorized is: \[ \dfrac{dy}{dt}=k(N-y) \] To solve, we separate variables and integrate: \[\begin{aligned} \int\dfrac{dy}{N-y}&=\int k\,dt \\ -\ln|N-y|&=kt+C \\ \ln|N-y|&=-kt+C \\ N-y&=\pm e^Ce^{-kt} \\ y&=N-Ae^{-kt} \\ \end{aligned}\] where $A=\pm e^C$. When $N=20$, the solution is: \[ y=20-Ae^{-kt} \] By plugging in the two given initial values, $y(1)=1$ and $y(3)=2$, we get two equations: \[ 1=20-Ae^{-k}\quad\text{and }\quad 2=20-Ae^{-3k} \] We first solve the first equation for $A$ in terms of $k$: \[\begin{aligned} Ae^{-k}&=19 \\ A&=19e^k \\ \end{aligned}\] We then substitute this expression into the second equation to solve for $k$: \[\begin{aligned} 2&=20-19e^{k}e^{-3k}=20-19e^{-2k} \\ e^{-2k}&=\dfrac{18}{19} \\ -2k&=\ln\left(\dfrac{18}{19}\right) \\ k&=.5\ln\left(\dfrac{19}{18}\right) \\ \end{aligned}\] We plug $k$ into the expression for $A$ and solve: \[\begin{aligned} A&=19e^{\textstyle .5\ln\left(\dfrac{19}{18}\right)} \\ &=19\left(\dfrac{19}{18}\right)^{.5} \\ &=19\sqrt{\dfrac{19}{18}} \\ \end{aligned}\]
  
  Plugging in both $A$ and $k$ to the general solution, we get: \[\begin{aligned} y&=20-19\sqrt{\dfrac{19}{18}}e^{\textstyle -.5\ln\left(\dfrac{19}{18}\right)t} \\ y&=20-19\left(\dfrac{19}{18}\right)^{.5-.5t} \\ \end{aligned}\] The plot for this solution is shown on the right.
  
  sy,jb
2. Solve the initial value problem using the logistic growth model. Plot the solution for $N=20$.
  
  Logarithmic Growth: \[ y_\text{log}=\dfrac{20}{1+19\left(\dfrac{19}{9}\right)^{.5-.5t}} \]
  
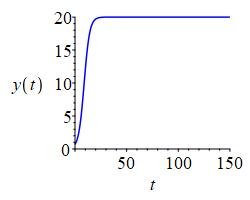
  We must solve the logistic growth model, $ \dfrac{dy}{dt}=ky(N-y) $, using the same given values. The general solution for the logistic growth model is: \[ y=\dfrac{N}{1+Be^{-Nkt}} \] where $B$ is a constant. We know $N=20$, so: \[ y=\dfrac{20}{1+Be^{-20kt}} \] By plugging in the two given initial values, $y(1)=1$ and $y(3)=2$, we get two equations: \[ 1=\dfrac{20}{1+Be^{-20k}}\quad\text{and }\quad 2=\dfrac{20}{1+Be^{-60k}} \] We first solve the first equation for $B$ in terms of $k$: \[\begin{aligned} 1+Be^{-20k}&=20 \\ B&=19e^{20k} \\ \end{aligned}\] We then plug in $B$ to the second equation to solve for $k$: \[\begin{aligned} 2&=\dfrac{20}{1+19e^{20k}e^{-60k}} \\ 10&=1+19e^{-40k} \\ e^{-40k}&=\dfrac{9}{19} \\ -40k&=\ln\left(\dfrac{9}{19}\right) \\ k&=.025\ln\left(\dfrac{19}{9}\right) \\ \end{aligned}\] We plug $k$ into the expression for $B$ and simplify: \[\begin{aligned} B&=19e^{\small 20(.025\ln(19/9))} \\ &=19e^{\small .5\ln(19/9)} \\ &=19\sqrt{\dfrac{19}{9}} \\ \end{aligned}\]
  
  Plugging in both $B$ and $k$ to the general solution, we get: \[\begin{aligned} y&=\dfrac{20}{1+19\sqrt{\dfrac{19}{9}}e^{\small -20(.025)\ln(19/9)t}} \\ &=\dfrac{20}{1+19\sqrt{\dfrac{19}{9}}e^{\small -.5\ln(19/9)t}} \\ &=\dfrac{20}{1+19\left(\dfrac{19}{9}\right)^{.5-.5t}} \\ \end{aligned}\] The plot for this solution is shown on the right.
  
  sy,jb
3. Compare the limited growth model with the logistic growth model.
  
  Comparing the limited growth model, $\dfrac{dy}{dt}=k(N-y)$, with the logistic growth model, $\dfrac{dy}{dt}=ky(N-y)$, we can see that in both models, $\dfrac{dy}{dt}\gt0$ provided $0 \lt y \lt N$, meaning that both models are ever increasing. The solutions are:
  
  Limited Growth: \[ y_\text{lim}=20-19\left(\dfrac{19}{18}\right)^{.5-.5t} \]
  
  Logarithmic Growth: \[ y_\text{log}=\dfrac{20}{1+19\left(\dfrac{19}{9}\right)^{.5-.5t}} \]
  
  We find the limiting value for each the model as $t$ approaches infinity. For the limited growth model: \[ \lim_{t\to\infty} y_\text{lim} =\lim_{t\to\infty} \left(20-19\left(\dfrac{19}{18}\right)^{.5-.5t}\right) =20 \] For the logistic growth model: \[ \lim_{t\to\infty} y_\text{lim} =\lim_{t\to\infty} \dfrac{20}{1+19\left(\dfrac{19}{9}\right)^{.5-.5t}} =20 \] So as $t$ approaches infinity, both models approach $20$ with the logarithmic model approaching faster.
  
  To find if and where they have an inflection point, we look at their second derivatives. For the limited growth model, the second derivative is: \[\begin{aligned} \dfrac{d^2y}{dt^2}&=\dfrac{d}{dt}\dfrac{dy}{dt} =\dfrac{d}{dt}\left[\rule{0pt}{10pt}k(N-y)\right] \\ &=-k\dfrac{dy}{dt} =-k^2(N-y) \end{aligned}\] Because $k\gt0$ and $N-y\gt0$, $\dfrac{d^2y}{dt^2}\lt0$, meaning that the limited growth model is concave down everywhere. It is important to note that $y=N$ is not an inflection point because the value of the function approaches $N$ (in this case, $N=20$), but $y$ never equals it.
  
  For the logistic growth model, the second derivative is: \[\begin{aligned} \dfrac{d^2y}{dt^2}&=\dfrac{d}{dt}\dfrac{dy}{dt} =\dfrac{d}{dt}\left[\rule{0pt}{10pt}ky(N-y)\right] \\ &=k\dfrac{dy}{dt}(N-y)-ky\dfrac{dy}{dt} \\ &=k\left[\rule{0pt}{10pt}ky(N-y)\right](N-y)-ky\left[\rule{0pt}{10pt}ky(N-y)\right] \\ &=k^2y(N-y)(N-2y) \end{aligned}\] Assuming $0\lt y\lt N$, setting this equal to zero and solving for $y$, we find that there is an inflection point at $y=\dfrac{N}{2}$. Given that $N=20$, the inflection point is at $y=10$. For $y\lt10$, the model is concave up. For $y\gt10$, the model is concave down. Again, $y=N$ is not an inflection point since it is a limiting value.
  
  For small values of $t$, the logistic growth model grows much faster than the limited growth model. But as $t$ gets large, both models approach the same value, $N=20$.
  
  sy,jb
An $8$ liter can contains $4$ liters of brine (salt water) with $3\,\dfrac{\text{g}}{\text{L}}$ of salt. Water containing $10\,\dfrac{\text{g}}{\text{L}}$ of salt is added at the rate of $2\,\dfrac{\text{L}}{\text{hr}}$. The solution is constantly mixed and is being withdrawn at $1.5\,\dfrac{\text{L}}{\text{hr}}$. (Notice that the rate of flow in is not equal to the rate of flow out.)
1. Give a differential equation satisfied by $S(t)$, the amount of salt in the container at time $t$ hours.
  
  What is the volume of brine as a function of time? (It's not constant.)
  
  $\dfrac{dS}{dt}=20-\dfrac{3S}{8+t}$
  
  In this problem, the volume is not contstant. $2\,\dfrac{\text{L}}{\text{hr}}$ are being added while $1.5\,\dfrac{\text{L}}{\text{hr}}$ are being removed. So the volume $V$ at time $t$ is: \[ V(t)=4+2t-1.5t=4+.5t \] Let $S(t)$ be the amount of salt in the can as a function of time. The differential equation for the rate of change of the amount of salt is: \[ \dfrac{dS}{dt} =10\,\dfrac{\text{g}}{\text{L}}\,2\,\dfrac{\text{L}}{\text{hr}} -\dfrac{S}{V}\,\dfrac{\text{g}}{\text{L}}\,1.5\,\dfrac{\text{L}}{\text{hr}} \] Substituting the volume in, we get: \[ \dfrac{dS}{dt}=20-\dfrac{1.5S}{4+.5t} =20-\dfrac{3S}{8+t} \]
  
  jb
2. Where does the amount of salt in the original solution enter into the problem?
  
  The original amount of salt is an initial condition. It is the product of the original concentration and the original volume. \[ S(0)=3\,\dfrac{\text{g}}{\text{L}}\cdot4\,\text{L}=12\,\text{g} \] It will be used to evaluate the constant of integration in the solution of the initial value problem.
3. Solve the initial value problem.
  
  $ S=5(8+t)-\dfrac{28\cdot8^3}{(8+t)^3} $
  
  We rewrite the differential equation in standard linear form: \[ \dfrac{dS}{dt}+\dfrac{3}{8+t}S=20 \] To solve, we find an integrating factor: \[ I=e^{\textstyle \int\frac{3}{8+t}dt}=e^{\textstyle 3\ln(8+t)} =(8+t)^3 \] We then multiply the standard linear form by the integrating factor on both sides: \[ (8+t)^3\dfrac{dS}{dt}+3(8+t)^2S=20(8+t)^3 \] We rewrite the left side as the derivative of a product, integrate both sides, and solve for $S$: \[\begin{aligned} \dfrac{d}{dt}\left[(8+t)^3S\right]&=20(8+t)^3 \\ (8+t)^3S&=\int20(8+t)^3dt=5(8+t)^4+C \\ S&=5(8+t)+\dfrac{C}{(8+t)^3} \\ \end{aligned}\] To solve for $C$, we plug in the initial value, $S=12$ when $t=0$: \[\begin{aligned} 12&=5(8)+\dfrac{C}{8^3} \\ -28&=\dfrac{C}{64} \\ C&=-28\cdot8^3 \\ \end{aligned}\] Plugging this in, we get: \[ S=5(8+t)-\dfrac{28\cdot8^3}{(8+t)^3} \]
  
  jb
4. Find the concentration of the solution at large times.
  
  $\displaystyle \lim_{t\to\infty}C(t)=10\,\dfrac{\text{g}}{\text{L}} $
  
  We first find the expression for $C(t)$, the concentration of salt as a function of time. To do this, we divide $S(t)$ by $V(t)$: \[\begin{aligned} C(t)&=\dfrac{S(t)}{V(t)} =\dfrac{1}{4+.5t}\left(5(8+t)-\dfrac{28\cdot8^3}{(8+t)^3}\right) \\ C(t)&=10-\dfrac{56\cdot8^3}{(8+t)^4} \end{aligned}\] To find the concentration of the solution at large times, we take the limit of the concentration as $t$ approaches infinity: \[ \lim_{t\to\infty}C(t) =\lim_{t\to\infty}\left(10-\dfrac{56\cdot8^3}{(8+t)^4}\right) =10\,\dfrac{\text{g}}{\text{L}} \]
  
  jb
A clay pot taken from a kiln has a temperature of $200^{\circ}F$. It is placed in a room at $72^{\circ}F$ to cool. After $1$ hour, the temperature has dropped to $136^{\circ}F$. Find the temperature $T$ of the pot as a function of time $t$ hours since removal from the kiln. How long will it take until the pot has cooled to $104^{\circ}F$.

$T(t)=72+128\cdot2^{-t}$
$t=2$ hours

Newton's law of heating says $\dfrac{dT}{dt}=-k(T-72)$ or equivalently, $\dfrac{d}{dt}(T-72)=-k(T-72)$. So the solution is: \[ T-72=Ae^{-kt} \] To solve for $A$, we plug in the inital value, $T(0)=200$: \[\begin{aligned} 200-72&=Ae^{-k(0)}\\ A&=128 \end{aligned}\] Plugging this in, we get: \[ T=72+128e^{-kt} \] To find $k$, we plug in $T(1)=136$: \[\begin{aligned} 136&=72+128^{-k} \\ e^{-k}&=\dfrac{136-72}{128} =\dfrac{1}{2} \\ -k&=\ln\dfrac{1}{2} \\ k&=\ln2\approx .693 \\ \end{aligned}\] Substituting this back in, we get: \[ T=72+128e^{-(\ln2)t}=72+128\cdot2^{-t} \] To find how long it will take until the pot has cooled to $104^{\circ}F$, we substitute $T=104$ and solve for $t$: \[\begin{aligned} 104&=72+128\cdot2^{-t} \\ 2^{-t}&=\dfrac{104-72}{128}=\dfrac{1}{4} \\ t&=2 \\ \end{aligned}\] Therefore, it will take $2$ hours for the pot to cool to $104^{\circ}F$.

sy,jb

PY: All Checked

8. Applications of Differential Equations

Exercises

a. Exponential Growth and Decay

b. Newtonian Heating and Cooling

c. Mixing Problems

d. A Robot Car

e. Falling near the Earth

f. Logistic Growth

Review Exercises

Heading